Solving ODE with Python
Ordinary Differential Equation
Let us consider the system of $\textbf{ODE}$ given by
\[\begin{equation} \dfrac{du}{dt} = Au + F(u, t) \quad on \quad [a, b], \end{equation}\]where $A\in \mathbb{R}^m \times \mathbb{R}^m$, $u \in \mathbb{R}$ and $F$ a non linear function
By multiplying the equation $(1)$ by the integrator factor $e^{-At}$, we have
\[\begin{align*} e^{-At}\dfrac{du}{dt} =& \; e^{-At}Au + e^{-At}F(u, t) \\ e^{-At}\dfrac{du}{dt} - e^{-At}Au =& \; e^{-At}F(u, t) \\ \dfrac{du}{dt}(ue^{-At}) =& \; e^{-At}F(u(t), t) \\ \int_{t_n}^{t_{n+1}} \dfrac{du}{dt}(ue^{-At})dt =& \; \int_{t_n}^{t_{n+1}} e^{-At}F(u(t), t)dt \\ \Longrightarrow \quad u(t_{n + 1})e^{-At_{n + 1}} - u(t_n)e^{-At_n} =& \; \int_{t_n}^{t_{n+1}} e^{-At}F(u(t), t)dt \\ u(t_{n + 1})e^{-At_{n + 1}} =& \; u(t_n)e^{-At_n} + \int_{t_n}^{t_{n+1}} e^{-At}F(u(t), t)dt \\ u(t_{n + 1}) =& \; u(t_n)e^{At_{n + 1}}e^{-At_n} + e^{At_{n + 1}}\int_{t_n}^{t_{n+1}} e^{-At}F(u(t), t)dt \\ u(t_{n + 1}) =& \; u(t_n)e^{A(t_{n+1}-t_n)} + \int_{t_n}^{t_{n+1}} e^{A(t_{n+1}-t)}F(u(t), t)dt \\ u(t_{n + 1}) =& \; u(t_n)e^{hA} + \int_{t_n}^{t_{n+1}} e^{A(t_{n+1}-t)}F(u(t), t)dt, \quad since \; h = t_{n+1} - t_n \\ \end{align*}\]Let $\tau = t - t_n \quad \Longrightarrow \quad d\tau = dt $
When
\[\begin{align*} t = t_n & \Rightarrow \tau = 0 \\ t = t_{n+1} & \Rightarrow \tau = t_{n+1} - t_n = h \\ \end{align*}\]So
\[\begin{align*} u(t_{n + 1}) =& \; u(t_n)e^{hA} + \int_0^h e^{A(t_{n+1}-(\tau + t_n))}F(u(\tau + t_n), \tau + t_n)d\tau \\ u(t_{n + 1}) =& \; u(t_n)e^{hA} + \int_0^h e^{A(h-\tau)}F(u(\tau + t_n), \tau + t_n)d\tau \\ u(t_{n + 1}) =& \; u(t_n)e^{hA} + \int_0^h e^{-(\tau - h)A}F(u(\tau + t_n), \tau + t_n)d\tau \\ \end{align*}\]Let $u_n \approx u(t_n)$, $F_n = F(u(t_n), t_n)$ and assume F is constant. Then we have \(\begin{align*} u(t_{n + 1}) =& \; u(t_n)e^{hA} + \int_0^h e^{-(\tau - h)A}F(u(\tau + t_n), \tau + t_n)d\tau \\ u(t_{n + 1}) =& \; u(t_n)e^{hA} + F\int_0^h e^{-(\tau - h)A}d\tau \\ u(t_{n + 1}) =& \; u(t_n)e^{hA} + Fe^{hA}\int_0^h e^{-\tau A}d\tau \\ u(t_{n + 1}) =& \; u(t_n)e^{hA} + Fe^{hA}\left[ -A^{-1}e^{-\tau A} \right]_{0}^{h} \\ u(t_{n + 1}) =& \; u(t_n)e^{hA} + Fe^{hA}\left[ -A^{-1}e^{-h A} + A^{-1} \right] \\ u(t_{n + 1}) =& \; u(t_n)e^{hA} + \left(e^{h A} - I \right)A^{-1}F \\[0.5cm] u_n \approx u(t_n) \quad and \quad F_n \approx F \quad \Longrightarrow \quad u_{n + 1} =& \; u_ne^{hA} + \left(e^{h A} - I \right)A^{-1}F_n \end{align*}\)
Importing package
import numpy as np
from scipy.linalg import inv
from scipy.linalg import expm
import matplotlib.pyplot as plt
Define function ExpoMethod
def ExpoMethod(a, b, A, F, h, u0):
m = len(u0)
#Generating partition
N = int((b-a)/h + 1)
T = np.linspace(a, b, N)
#Computing some constant of the method
ehA = expm(h*A)
I = np.identity(m)
A_inv = inv(A)
c = (ehA - I)@A_inv
#Create a matrix such that each column is a solution of the method
U = np.zeros( (N, m) )
U[0] = u0
for n in range(N-1):
U[n + 1] = ehA@U[n] + c@F(U[n], T[n])
return U, T
Let us consider the system of ODE
\[\begin{equation} \dfrac{du}{dt} = Au \quad u(0) = u_0 \end{equation}\]With
\[A = \begin{pmatrix} 2 & 2 & 1 \\ 1 & 3 & 1 \\ 1 & 2 & 2 \end{pmatrix}\]and
\[u_0 = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}\]The exact solution of the equation is:
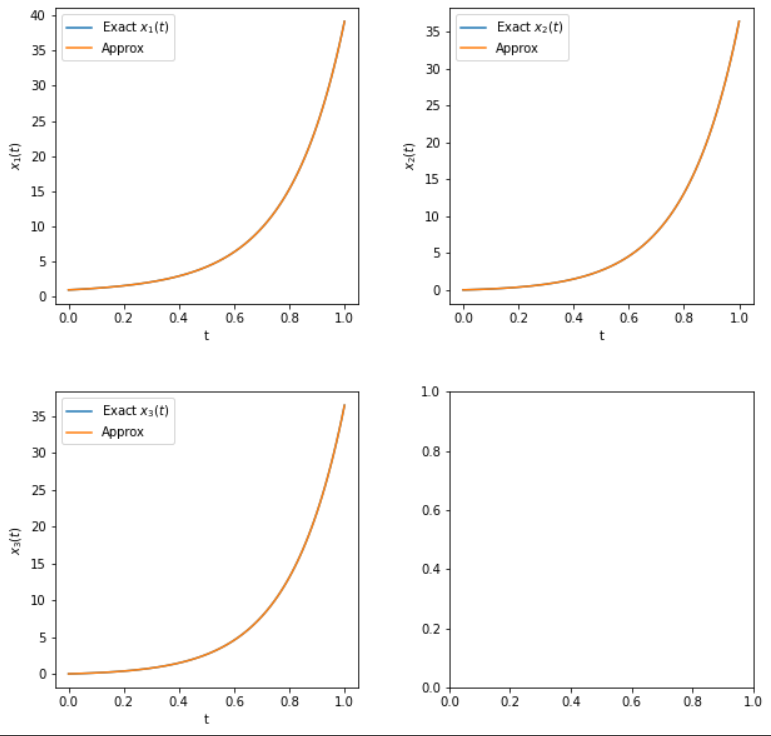
\[x(t) = \begin{pmatrix} \dfrac{3}{4}e^t + \dfrac{1}{4}e^{5t} \\ -\dfrac{1}{4}e^t + \dfrac{1}{4}e^{5t} \\ -\dfrac{1}{4}e^t + \dfrac{1}{4}e^{5t} \end{pmatrix}\]Define code plot the exact solution and the approximation of the equation above, using the function ExpoMethod
def exact(t):
x1 = ((3/4)*np.exp(t) + (1/4)*np.exp(5*t))
x2 = ((1/4)*np.exp(5*t) - (1/4)*np.exp(t))
x3 = x2
return np.array([x1, x2, x3])
# Define the function F like a null vector
def F(u,t):
return np.array([0, 0, 0])
#parameters
a = 0
b = 1
h = 0.01
#initial condition
u0 = np.array([1, 0, 0])
#matrix of the system
A = np.array([
[2, 2, 1],
[1, 3, 1],
[1, 2, 2]])
#The approximation and time
u, t = ExpoMethod(a, b, A, F, h, u0)
#Exact solution
x = exact(t)
#plot
fig, axes = plt.subplots(2, 2,figsize=(10,10))
plt.subplots_adjust(hspace=0.3, wspace=0.3)
axes[0,0].plot(t, x[0], t, u[:,0])
axes[0,0].set_xlabel('t')
axes[0,0].set_ylabel('$x_1(t)$')
axes[0,0].legend(['Exact $x_1(t)$', 'Approx'],loc='upper left')
axes[0,1].plot(t, x[1], t, u[:,1])
axes[0,1].set_xlabel('t')
axes[0,1].set_ylabel('$x_2(t)$')
axes[0,1].legend(['Exact $x_2(t)$', 'Approx'],loc='upper left')
axes[1,0].plot(t, x[2], t, u[:,2])
axes[1,0].set_xlabel('t')
axes[1,0].set_ylabel('$x_3(t)$')
axes[1,0].legend(['Exact $x_3(t)$', 'Approx'],loc='upper left')
plt.show()
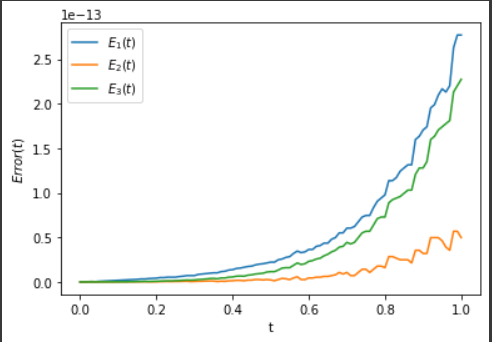
Absolute Errors
# Errors
E1 = abs(x[0] - u[:, 0])
E2 = abs(x[1] - u[:, 1])
E3 = abs(x[2] - u[:, 2])
plt.plot(t, E1, t, E2, t, E3)
plt.xlabel('t')
plt.ylabel('$Error(t)$')
plt.legend(['$E_1(t)$', '$E_2(t)$', '$E_3(t)$'],loc='upper left')
plt.show()